Is it time to bury the h-index?

Ian Rowlands hammers another nail into the h-index’s coffin by explaining how it actually brings nothing new to the table and by showing how chance determines its outcome.

The poor old h-index has come in for a lot of criticism recently, with a flood of papers pointing to its conceptual and practical shortcomings.  Is it time to bury it?  Cameron Barnes, an academic at the University of New England, New South Wales thinks so, because he has just written a devastating critique for library practitioners (Barnes 2017).  I strongly recommend his article to anyone hoping to advance the cause of responsible metrics.

The aim of this post is not to rehearse Cameron’s arguments – better you get them direct from the horse’s mouth.  I want to pour some more petrol on the funeral pyre by approaching the topic from another angle using first principles.  I hope to show that the h-index provides information that is almost completely redundant for most practical purposes, and that because of the way it is constructed, chance plays a significant role in determining its outcome.

On the face of it, it is an attractive indicator because it summarises a lot of information and it purports to tell us something about both productivity, quality and consistency.

Just a quick recap: the h-index is a composite indicator based on the pattern of an author’s papers and their citations: a scientist with an h-index of ten must be able to point to ten papers cited at least ten or more times each.  The index obviously cannot be larger than the total number of his or her papers and is invariably smaller, because papers vary in terms of their impact.  On the face of it, it is an attractive indicator because it summarises a lot of information and it purports to tell us something about both productivity, quality and consistency.

The h-index is redundant for most practical purposes

Given the building blocks, it is hardly surprising that h correlates strongly with numbers of both papers and citations.  This should come as no surprise, but I’m not sure that many practitioners or users realise quite how strong those relationships are, nor have they yet grasped the implications.

Here’s a chart I created for 163 genetics researchers, plotting their career h-index against the square root of their total citations:

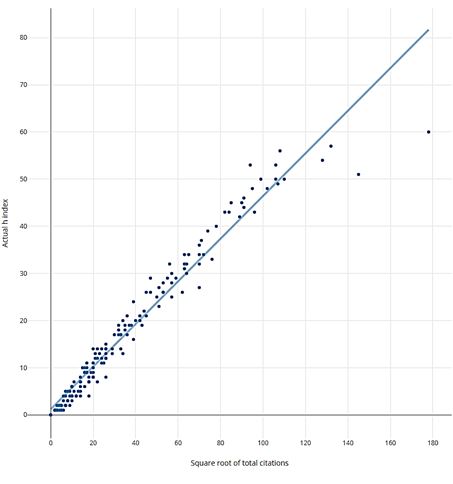
The linear fit is so convincing (R²=0.96) that you might well ask whether h adds anything new to the conversation? Why go the bother of working out h, a real pain, when you can easily find total citations?  From this evidence – and you can find many charts like this in the literature – it seems to me the best you can say is that h offers a pretty good estimate of total citation impact.  Do we need this?

Chance effects and the h-index

Looking again at the graph, though, I can’t fail to be surprised that so many researchers sit on or very close to the trend line.  The h index is supposed to tell us something useful about differences between researchers – and they are a diverse bunch indeed.  Many are productive in bursts, possibly early or late in their career.  Some are remarkably consistent over their full career. For others, their publishing career may be interrupted by administrative burdens, caring responsibilities, or ill health.

Can the straight line be explained?  I think it can, using a simple probabilistic framework. Let’s work through a theoretical example: a scientist, Ayeesha, with ten papers and 100 citations. From first principles we know that her h-index must be at least one but it can’t be larger than ten.  My question then becomes: are all ten possible h outcomes equally likely?

There are relatively few combinations of citations per paper that satisfy h=1.

We could have:

{100, 0, 0, 0, 0, 0, 0, 0, 0, 0}

or

{99, 1, 0, 0, 0, 0, 0, 0, 0, 0}

or

{98, 1, 1, 0, 0, 0, 0, 0, 0, 0}

There are of course seven further possible combinations: ten in all.

At the other end of the scale, h=10, there is only one possible combination that works for this particular researcher:

{10, 10, 10, 10, 10, 10, 10, 10, 10, 10}

It would be very surprising indeed to find a researcher with this number of papers and citations returning an h-index of 1 or 10 in real life, but that’s not my point here.  I’m only interested in the properties of the scale.

Moving on to h=2, the number of possible combinations really starts to open up.  We could have:

{98, 2, 0, 0, 0, 0, 0, 0, 0, 0}

or

{46, 46, 1, 1, 1, 1, 1, 1, 1, 1}

or indeed any other combination which met the condition that any of the bottom eight papers can either have 1 or 0 citations, while the top two must share the remainder (at least 92) in whatever proportion.  That’s quite a lot, but by the time you get to the mid-point in the theoretical range, the number of hypothetical combinations that satisfy h=5 or h=6 becomes very, very large indeed.

Where is all this going?  Well, if you were to generate a random publication profile based on 10 papers and 100 citations, you would be very, very much more likely to find that profile satisfying h=5 than h=2, simply on the grounds of probability: the fact is the h=5 net is far, far bigger than the h=2 net. This property of the scale must mean that h-values tend to flock together in the middling portion of the theoretically available scale, hence the straight line on my graph.

This has big responsible metrics implications.  If we compare two individuals on the basis of their h-index, how should we decide if the values are “similar”, “comparable”, or “very different”?

Consider now a second researcher, Tim, of similar age, ability and impact, also with ten papers and 100 citations.  Tim is a late developer and most of his publications bunch in the last eighteeen months.  Ayeesha has a very different profile.  After an early burst of productivity, she was promoted and took on heavy administrative duties as a course convenor.  She’s only recently started to publish again.  So, even if all the papers by Tim and Ayeesha are of equivalent quality, the chances are that Ayeesha will have a substantially higher h-index than Tim, just because the profile of her papers is older.  Are we really measuring quality here?

This is the main weakness of the h-index for me, publication patterns over a career are complex, and some of the differences between Tim and Ayeesha ought really be regarded as statistical noise in this particular context.

This has big responsible metrics implications.  If we compare two individuals on the basis of their h-index, how should we decide if the values are “similar”, “comparable”, or “very different”? Alexander Yong has calculated theoretical 95% confidence intervals for the h-index to try to inform this question (Yong 2014):

Total career citations	50	100	500	1,000	2,500	5,000	10,000
Interval for h	[2, 5]	[3, 7]	[9, 14]	[13, 20]	[22, 31]	[34, 43]	[47, 60]

(Adapted from Yong, 2014.)

This exposes another unexpected property of the h-index: the more senior an academic, and the greater their number of citations, the wider the confidence intervals needed to put h into its proper context.  This follows inevitably from the properties of the scale: by the time you get to h=50, say, the number of possible paper-citation combinations becomes absolutely huge.

In conclusion

Is it time to bury the h-index? As a practitioner my feeling is a definite yes, and with good riddance.  No one seems terribly clear what it actually indicates (productivity, quality, consistency, longevity, career trajectory?), but the empirical evidence suggests to me that h really brings nothing new to the table.  The index is highly platform-, field-, and time-dependent, making it next to useless for making responsible comparisons. A new reason to fret, once you start to think about the properties of the scale, is that chance factors, quite unrelated to quality, can play a significant role.  This has frightful implications for interpretation.  Given a researcher with 5,000 citations, you really ought to conclude, on the basis of Alexander Yong’s table above, that an h-index of 34 is broadly similar, within a 95% confidence interval, to an h-index of 43.

We could live with this kind of variation if we were just comparing researchers within the same field, but that’s not how things usually pan out.  What if a computer scientist (with an interest in molecular biology) is up against an immunologist (with an interest in bioinformatics) for the same job?  Citation rates in computer science and immunology are very different, to the extent that if you do the normalisation, a computer scientist with an h-index of 20 is of equivalent standing to an immunologist with h=54 (see Iglesias and Pecharroman, 2007, for normalisation tables based on broad ISI categories).

I wonder whether these consideration ever cross anyone’s mind on a promotions panel?

REQUIESCAT IN PACE!

References

Cameron Barnes (2017). The h-index debate: An introduction for librarians,  The Journal of Academic Librarianship 43(6): 487-494. http://dx.doi.org/10.1016/j.acalib.2017.08.013

Juan Iglesias and Carlos Pecharroman (2007). Scaling the h-index for different ISI fields, Scientometrics 73(3): 303-320. http://dx.doi.org/10.1007/s11192-007-1805-x

Alexander Yong (2014).  Critique of Hirsch’s h index: A combinatorial fermi problem, Notices of the American Mathematical Society 61(9): 1040-1050. http://dx.doi.org/10.1090/noti1164

• The article has been updated on 27.03.18 to reflect additional information within the conclusion.

---

Dr Ian Rownland is the Research Information & Intelligence Specialist at King’s College London.  After teaching information science at City University London and UCL for twenty years, he turned gamekeeper five years’ ago and moved into professional services to practice the dark arts, initially at the University of Leicester.  The main thrust of the role at King’s is helping to raise the ‘metrics literacy’ bar and to offer practical guidance on correct interpretation of bibliometric and other research indicators.

 

 

Unless it states other wise, the content of the Bibliomagician is licensed under a Creative Commons Attribution 4.0 International License.